展示实体

属性 [编辑]

介绍 [编辑]

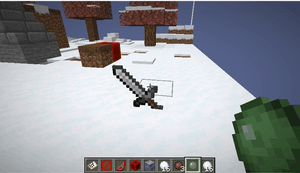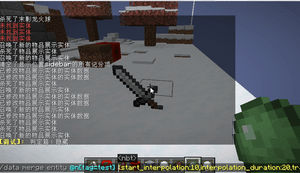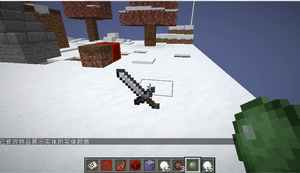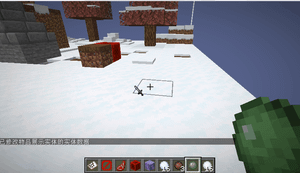
1. 展示实体（Display）是用于多样内容展示的实体类型，主要包括方块展示实体（Block Display）、物品展示实体（Item Display）和文本展示实体（Text Display），各自用于展示方块、物品及文本内容。

2. 展示实体本身不具备移动能力，即使指定了**Motion字段，它们也不会受到伤害、发出声音、影响方块放置，也不会推开玩家或其他实体。

3. 当使用调试组合键F3 + B时，展示实体不会显示出判定箱，但会展现表示其朝向的蓝色线段。

4. 由于展示实体无法被选中，因此无法通过F3 + I功能将其实体数据复制到剪贴板。

5. 利用不带实体数据参数的/summon命令生成的展示实体是不可见的，对于方块展示实体和物品展示实体，其默认展示内容分别为{block_state:{Name:"minecraft:air"} }及{item:{id:"minecraft:air",count:1} }，而文本展示实体的默认内容则是{"text": ""}。

6. 通过修改实体数据，能够设置展示的具体内容及其他视觉效果，并对模型进行旋转、缩放和平移调整。

7. 针对物品展示实体，除了可以使用/data操作来修改实体数据外，亦可采用/loot或/item命令在container.0槽位进行物品的获取与更换。

8. 物品展示实体通过物品堆叠组件item_model，能够轻松展示任何自定义的物品模型。

生成 [编辑]

1. 方块展示实体、物品展示实体和文本展示实体不会生成在世界中，但可以使用/summon等命令生成。

行为 [编辑]

一、 插值

1. 在Minecraft中，对于展示实体属性的变化，可以通过插值技术实现渐变动画效果。

2. 所有被标记为“可插值”的属性都可以用于生成这些变化过程的插值动画。

3. 客户端会记录实体生成后，这些“可插值”属性在变化前后的数值。

4. 插值处理将综合考虑变化前后的所有属性。

5. 每个游戏刻中，服务器与客户端之间最多只能同步一次实体数据，因此即便在同一刻内发生多次变化，它们也被视为单次变更。

6. 实体的渲染效果会随着插值时间的推移而产生渐变。

7. 客户端会在接收到并经过start_interpolation游戏刻后，开始执行插值过程。

8. 此插值过程将持续时间为interpolation_duration的游戏刻，总共需要的时间为start_interpolation与interpolation_duration之和。

二、 变换

1. 当使用矩阵数据时，在游戏加载的过程中，会将矩阵进行分解，而非直接应用于变换操作。

2. 具体来说，将矩阵M拆分为三个部分，表示为𝐌=(𝐑3×3𝐭3×1w1×1)。

3. 然后，矩阵R和向量t会依据1/w进行缩放处理，得出𝐑′=1/w𝐑和𝐭′=1/w𝐭。

4. 缩放后的向量t'将表示平移变换。

5. 接下来，对矩阵R'进行奇异值分解，得到𝐑′=𝐔Σ𝐕T，其中矩阵U代表左旋转，矩阵𝐕T则代表右旋转，而这两个矩阵将转换为相应的单位四元数。

6. 另外，对角矩阵Σ的主对角线部分则表示缩放的相关信息。

7. 实际上，模型最终的变换可以表示为(𝐑′ 𝐭′)（3x4矩阵），其中原矩阵左下角的1x3部分并不起作用；当w等于1时，该变换可简化为矩阵数据前12个值对模型变换的影响。

8. 假设模型中某一点的坐标为(x,y,z)，经过变换后的位置表述为(𝐑′ 𝐭′)(x,y,z,1)T。

9. 如果采用分解形式进行处理，游戏会将相应的数据直接设置为实体数据的值。

10. 在分解形式中，涉及到的两个旋转数据的定义，假定以四元数的形式表示，即q=w+xi+yj+zk（其在数据中的表现为[x, y, z, w]）。

11. 当q为单位四元数时，该四元数所代表的旋转是围绕(x,y,z)向量的旋转轴，逆时针旋转的角度为2arccosw。

12. 若q不是单位四元数，则需进行计算q=|q|e，其中e为单位四元数所表示的旋转；同时，整个模型的缩放因子为|q|²。

13. 不论四元数是否为单位形式，游戏都会采用此四元数来计算旋转及其可能的缩放。

14. 如果用轴-角度形式定义旋转，则游戏会将其转化为单位四元数表示：设轴为𝐚=(x,y,z)，旋转角度为θ。

15. 游戏首先将轴的单位向量计算为𝐚=|a|𝐞，接着根据四元数规则构造旋转单位四元数q=cos⁡(θ/2)+sin⁡(θ/2)(𝐞xi+𝐞yj+𝐞zk)。

16. 在游戏渲染过程中，模型经历右旋转、缩放、左旋转及平移等变换步骤。

17. 在这个过程中，左右旋转均以单位四元数的形式存在，而非单位四元数的旋转其缩放系数与缩放数据相乘，并在缩放步骤中一同进行计算。

18. 假设模型中的某一点为(x,y,z)，可以构造纯四元数p0=xi+yj+zk。

19. 使用右旋转四元数qr进行旋转后，得出p1=qrp0qr−1。

20. 接下来，按照各坐标轴应用缩放数据𝐬，得到p2=𝐬xp1xi+𝐬yp1yj+𝐬zp1zk。

21. 之后，运用左旋转四元数ql进行第二次旋转，p3=qlp2ql−1。

22. 最终，经过平移向量𝐭变换后，坐标结果为𝐩=(p3x,p3y,p3z)+𝐭。

23. 在这个变换过程中，若右旋转四元数等于1（不进行旋转），或不实施缩放，则模型在变换后仍能保持各顶点之间的相对位置不变，从而不发生变形。

24. 报告的步骤显示，右旋转与缩放共同影响模型的变形，缩放决定模型的大小，左旋转则影响模型的最终朝向，而平移决定模型的位置。

25. 当渲染变换被更改时，游戏会进行插值以实现两次不同变换间的平滑过渡。

26. 在此，当前的插值进度为p：对于平移与缩放，游戏采用线性插值（Linear Interpolation），即𝐯=p𝐯1+(1−p)𝐯0。

27. 而在旋转（四元数）的情况下，游戏使用球面线性插值（Spherical Linear Interpolation），计算公式为θ=arccos(q0⋅q1), q=1/sin⁡θ(sin⁡(pθ)q1+sin⁡((1−p)θ)q0)。

数据值 [编辑]

一、 ID

Java版：

实体	命名空间ID	本地化键名
方块展示实体	block_display	entity.minecraft.block_display
物品展示实体	item_display	entity.minecraft.item_display
文本展示实体	text_display	entity.minecraft.text_display

其他

来自:我的世界百科  物品

其他

来自:我的世界百科  方块

其他

来自:我的世界百科  实体